template<class CAMERA>
class gtsam::RegularImplicitSchurFactor< CAMERA >
RegularImplicitSchurFactor.
|
|
| RegularImplicitSchurFactor () |
| | Constructor.
|
| |
|
| RegularImplicitSchurFactor (const KeyVector &keys, const std::vector< MatrixZD, Eigen::aligned_allocator< MatrixZD > > &FBlocks, const Matrix &E, const Matrix &P, const Vector &b) |
| | Construct from blocks of F, E, inv(E'*E), and RHS vector b.
|
| |
|
virtual | ~RegularImplicitSchurFactor () |
| | Destructor.
|
| |
|
std::vector< MatrixZD, Eigen::aligned_allocator< MatrixZD > > & | FBlocks () const |
| |
|
const Matrix & | E () const |
| |
|
const Vector & | b () const |
| |
|
const Matrix & | getPointCovariance () const |
| |
|
void | print (const std::string &s="", const KeyFormatter &keyFormatter=DefaultKeyFormatter) const |
| | print
|
| |
|
bool | equals (const GaussianFactor &lf, double tol) const |
| | equals
|
| |
|
virtual DenseIndex | getDim (const_iterator variable) const |
| | Degrees of freedom of camera.
|
| |
| virtual void | updateHessian (const KeyVector &keys, SymmetricBlockMatrix *info) const |
| | Update an information matrix by adding the information corresponding to this factor (used internally during elimination). More...
|
| |
| virtual Matrix | augmentedJacobian () const |
| | Return a dense \( [ \;A\;b\; ] \in \mathbb{R}^{m \times n+1} \) Jacobian matrix, augmented with b with the noise models baked into A and b. More...
|
| |
| virtual std::pair< Matrix, Vector > | jacobian () const |
| | Return the dense Jacobian \( A \) and right-hand-side \( b \), with the noise models baked into A and b. More...
|
| |
|
virtual Matrix | augmentedInformation () const |
| | Compute full augmented information matrix
|
| |
|
virtual Matrix | information () const |
| | Compute full information matrix
|
| |
|
virtual VectorValues | hessianDiagonal () const |
| | Return the diagonal of the Hessian for this factor.
|
| |
|
virtual void | hessianDiagonal (double *d) const |
| | add the contribution of this factor to the diagonal of the hessian d(output) = d(input) + deltaHessianFactor
|
| |
|
virtual std::map< Key, Matrix > | hessianBlockDiagonal () const |
| | Return the block diagonal of the Hessian for this factor.
|
| |
|
virtual GaussianFactor::shared_ptr | clone () const |
| | Clone a factor (make a deep copy)
|
| |
|
virtual bool | empty () const |
| | Test whether the factor is empty.
|
| |
| virtual GaussianFactor::shared_ptr | negate () const |
| | Construct the corresponding anti-factor to negate information stored stored in this factor. More...
|
| |
|
void | projectError2 (const Error2s &e1, Error2s &e2) const |
| | Calculate corrected error Q*(e-ZDim*b) = (I - E*P*E')*(e-ZDim*b)
|
| |
|
virtual double | error (const VectorValues &x) const |
| | Print for testable.
|
| |
|
double | errorJF (const VectorValues &x) const |
| |
|
void | projectError (const Error2s &e1, Error2s &e2) const |
| | Calculate corrected error Q*e = (I - E*P*E')*e.
|
| |
| void | multiplyHessianAdd (double alpha, const double *x, double *y) const |
| | double* Hessian-vector multiply, i.e. More...
|
| |
|
void | multiplyHessianAdd (double alpha, const double *x, double *y, std::vector< size_t > keys) const |
| |
| void | multiplyHessianAdd (double alpha, const VectorValues &x, VectorValues &y) const |
| | Hessian-vector multiply, i.e. More...
|
| |
|
void | multiplyHessianDummy (double alpha, const VectorValues &x, VectorValues &y) const |
| | Dummy version to measure overhead of key access.
|
| |
|
VectorValues | gradientAtZero () const |
| | Calculate gradient, which is -F'Q*b, see paper.
|
| |
|
virtual void | gradientAtZero (double *d) const |
| | Calculate gradient, which is -F'Q*b, see paper - RAW MEMORY ACCESS.
|
| |
|
Vector | gradient (Key key, const VectorValues &x) const |
| | Gradient wrt a key at any values.
|
| |
|
| GaussianFactor () |
| | Default constructor creates empty factor.
|
| |
| template<typename CONTAINER > |
| | GaussianFactor (const CONTAINER &keys) |
| | Construct from container of keys. More...
|
| |
|
virtual | ~GaussianFactor () |
| | Destructor.
|
| |
|
Key | front () const |
| | First key.
|
| |
|
Key | back () const |
| | Last key.
|
| |
|
const_iterator | find (Key key) const |
| | find
|
| |
|
const KeyVector & | keys () const |
| | Access the factor's involved variable keys.
|
| |
|
const_iterator | begin () const |
| | Iterator at beginning of involved variable keys.
|
| |
|
const_iterator | end () const |
| | Iterator at end of involved variable keys.
|
| |
| size_t | size () const |
| |
|
void | print (const std::string &s="Factor", const KeyFormatter &formatter=DefaultKeyFormatter) const |
| | print
|
| |
|
void | printKeys (const std::string &s="Factor", const KeyFormatter &formatter=DefaultKeyFormatter) const |
| | print only keys
|
| |
| KeyVector & | keys () |
| |
|
iterator | begin () |
| | Iterator at beginning of involved variable keys.
|
| |
|
iterator | end () |
| | Iterator at end of involved variable keys.
|
| |
|
|
| Factor () |
| | Default constructor for I/O.
|
| |
| template<typename CONTAINER > |
| | Factor (const CONTAINER &keys) |
| | Construct factor from container of keys. More...
|
| |
| template<typename ITERATOR > |
| | Factor (ITERATOR first, ITERATOR last) |
| | Construct factor from iterator keys. More...
|
| |
|
bool | equals (const This &other, double tol=1e-9) const |
| | check equality
|
| |
| template<typename CONTAINER > |
| static Factor | FromKeys (const CONTAINER &keys) |
| | Construct factor from container of keys. More...
|
| |
| template<typename ITERATOR > |
| static Factor | FromIterators (ITERATOR first, ITERATOR last) |
| | Construct factor from iterator keys. More...
|
| |
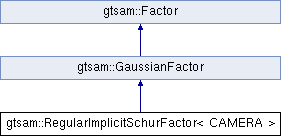
 Inheritance diagram for gtsam::RegularImplicitSchurFactor< CAMERA >:
Inheritance diagram for gtsam::RegularImplicitSchurFactor< CAMERA >: Public Member Functions inherited from gtsam::GaussianFactor
Public Member Functions inherited from gtsam::GaussianFactor Public Member Functions inherited from gtsam::Factor
Public Member Functions inherited from gtsam::Factor Static Public Member Functions inherited from gtsam::GaussianFactor
Static Public Member Functions inherited from gtsam::GaussianFactor Public Types inherited from gtsam::GaussianFactor
Public Types inherited from gtsam::GaussianFactor Public Types inherited from gtsam::Factor
Public Types inherited from gtsam::Factor Protected Attributes inherited from gtsam::Factor
Protected Attributes inherited from gtsam::Factor Protected Member Functions inherited from gtsam::Factor
Protected Member Functions inherited from gtsam::Factor Static Protected Member Functions inherited from gtsam::Factor
Static Protected Member Functions inherited from gtsam::Factor