True SO(3), i.e., 3*3 matrix subgroup We guarantee (all but first) constructors only generate from sub-manifold.
However, round-off errors in repeated composition could move off it...
|
|
Matrix3 | AdjointMap () const |
| |
|
static SO3 | Expmap (const Vector3 &omega, ChartJacobian H=boost::none) |
| | Exponential map at identity - create a rotation from canonical coordinates \( [R_x,R_y,R_z] \) using Rodrigues' formula.
|
| |
|
static Matrix3 | ExpmapDerivative (const Vector3 &omega) |
| | Derivative of Expmap.
|
| |
|
static Vector3 | Logmap (const SO3 &R, ChartJacobian H=boost::none) |
| | Log map at identity - returns the canonical coordinates \( [R_x,R_y,R_z] \) of this rotation.
|
| |
| static Matrix3 | LogmapDerivative (const Vector3 &omega) |
| | Derivative of Logmap. More...
|
| |
|
|
|
void | print (const std::string &s) const |
| |
|
bool | equals (const SO3 &R, double tol) const |
| |
|
| BOOST_STATIC_ASSERT_MSG (N !=Eigen::Dynamic, "LieGroup not yet specialized for dynamically sized types.") |
| |
|
const SO3 & | derived () const |
| |
|
SO3 | compose (const SO3 &g) const |
| |
|
SO3 | compose (const SO3 &g, ChartJacobian H1, ChartJacobian H2=boost::none) const |
| |
|
SO3 | between (const SO3 &g) const |
| |
|
SO3 | between (const SO3 &g, ChartJacobian H1, ChartJacobian H2=boost::none) const |
| |
|
SO3 | inverse (ChartJacobian H) const |
| |
|
SO3 | expmap (const TangentVector &v) const |
| | expmap as required by manifold concept Applies exponential map to v and composes with *this
|
| |
|
SO3 | expmap (const TangentVector &v, ChartJacobian H1, ChartJacobian H2=boost::none) const |
| | expmap with optional derivatives
|
| |
|
TangentVector | logmap (const SO3 &g) const |
| | logmap as required by manifold concept Applies logarithmic map to group element that takes *this to g
|
| |
|
TangentVector | logmap (const SO3 &g, ChartJacobian H1, ChartJacobian H2=boost::none) const |
| | logmap with optional derivatives
|
| |
|
SO3 | retract (const TangentVector &v) const |
| | retract as required by manifold concept: applies v at *this
|
| |
|
SO3 | retract (const TangentVector &v, ChartJacobian H1, ChartJacobian H2=boost::none) const |
| | retract with optional derivatives
|
| |
|
TangentVector | localCoordinates (const SO3 &g) const |
| | localCoordinates as required by manifold concept: finds tangent vector between *this and g
|
| |
|
TangentVector | localCoordinates (const SO3 &g, ChartJacobian H1, ChartJacobian H2=boost::none) const |
| | localCoordinates with optional derivatives
|
| |
| Matrix3 gtsam::SO3::LogmapDerivative |
( |
const Vector3 & |
omega | ) |
|
|
static |
Derivative of Logmap.
Right Jacobian for Log map in SO(3) - equation (10.86) and following equations in G.S. Chirikjian, "Stochastic Models, Information Theory, and Lie Groups", Volume 2, 2008. logmap( Rhat * expmap(omega) ) \approx logmap( Rhat ) + Jrinv * omega where Jrinv = LogmapDerivative(omega); This maps a perturbation on the manifold (expmap(omega)) to a perturbation in the tangent space (Jrinv * omega)
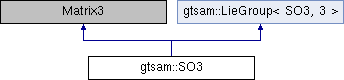
 Inheritance diagram for gtsam::SO3:
Inheritance diagram for gtsam::SO3: Public Member Functions inherited from gtsam::LieGroup< SO3, 3 >
Public Member Functions inherited from gtsam::LieGroup< SO3, 3 > Public Types inherited from gtsam::LieGroup< SO3, 3 >
Public Types inherited from gtsam::LieGroup< SO3, 3 > Static Public Member Functions inherited from gtsam::LieGroup< SO3, 3 >
Static Public Member Functions inherited from gtsam::LieGroup< SO3, 3 >