Author: Fan Jiang

Introduction

You are probably here because you do optimization, like everyone here on the GTSAM team. As fellow roboticists, we know how frustrating it be when your problem does not converge.

To further optimize your optimization experience, we are excited to announce this new release of GTSAM, GTSAM 4.0.3, where we incorporated a lot of new features and bugfixes, as well as substantial improvements in convergence for Pose3-related problems.

Note that GTSAM already provides the excellent Pose3 initialization module by Luca Carlone, in InitializePose3, which we always recommend if your pipeline does not provide a good initial estimate out of the box.

Major Changes

Switching Away from Cayley

TL;DR: GTSAM will now default to using the full $\mathrm{SE(3)}$ exponential map, instead of using the Cayley map, which should give better convergence for most problems without performance impact.

In nonlinear optimization, one important factor affecting the convergence is the mathematical structure of the object we are optimizing on. In many practical 3D robotics problems this is the $\mathrm{SE(3)}$ manifold describing the structure of 3D Poses.

It is not easy to directly operate on nonlinear manifolds like $\mathrm{SE(3)}$, so libraries like GTSAM uses the following strategy:

• Linearize the error manifold at the current estimate
• Calculate the next update in the associated tangent space
• Map the update back to the manifold with a retract map

We used two distinct but equally important concepts above: 1) the error metric, which is in a PoseSLAM problems is the measure of error between two poses; and 2) the retract operation, which is how we apply a computed linear update back to the nonlinear error manifold.

In GTSAM, you can choose, at compile time, between four different choices for the retract map on the $\mathrm{SE(3)}$ manifold:

• Full: Exponential map on $\mathrm{SE(3)}$
• Decomposed retract, which uses addition for translation and:
  • Exponential map $\mathrm{SO(3)}$ with Rotation Matrix
  • Exponential map $\mathrm{SO(3)}$ with Quaternions
  • Cayley map on $\mathrm{SO(3)}$ with Rotation Matrix

Previously in GTSAM, we used the Cayley map by default, which is an approximation of the $\mathrm{SO(3)}$ exponential map when the tangent vector (rotation error) is small. This is perfectly fine locally, if we have a relatively good initial estimate.

However, since we are also using the inverse of the retract as the error metric, a different choice for the retract map could give better convergence. As you can see in the following figure, the Cayley local map is unbounded when $\theta$ is large, and thus negatively impacts convergence when the initialization is not good enough.

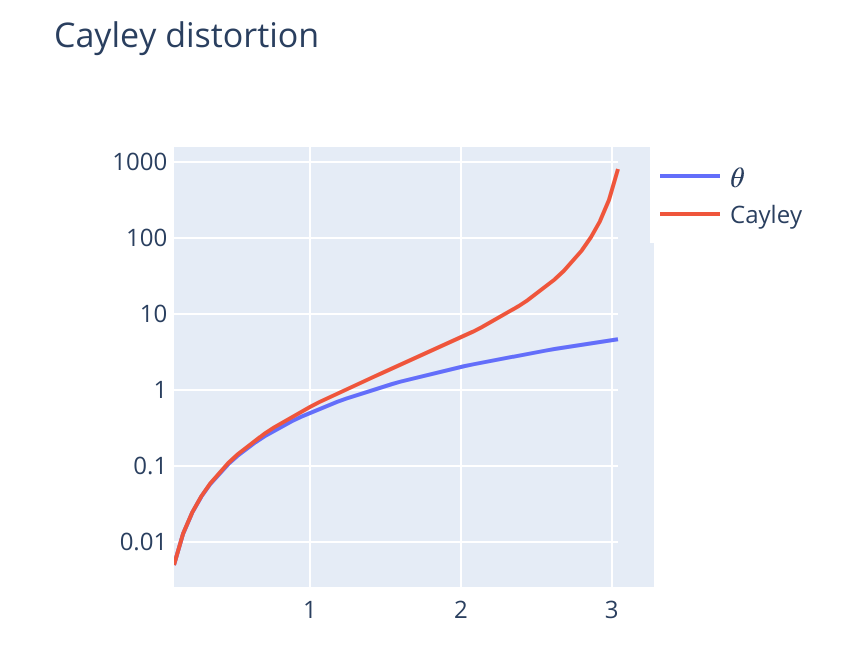
Based on careful benchmarking, in the new release, we will not use the Cayley approximation by default, which should give you a better convergence for most applications. This is especially true if your initial estimate can be far away from the global optimum: the impact on well-initialized problems is minimal. You can look at the benchmark yourself in the next section, if you are interested.

Can we still use Cayley and Friends?

Yes, just not by default. Historically, the Cayley approximation was chosen as a cheaper alternative to the full exponential map, and our intention is not to tell you that you should not use it, rather to inform you that without properly initializing your initial estimate, the result of Cayley could be inferior to those obtained with the full $\mathrm{SE(3)}$ retract.

In order to give you an intuitive understanding of the situation we made a benchmark where the four configurations by:

• asking GTSAM to solve 6 benchmark optimization datasets, with the Chordal initialization as initial estimate (from InitializePose3);
• asking GTSAM to solve 6 benchmark optimization datasets, this time with 100 random initial estimates, sampled around the ground truth by a Gaussian distribution of 1 sigma, and observe the convergence metrics.

Note that with proper initialization, all 4 configurations achieved convergence without issue. However, the full $\mathrm{SE(3)}$ retract exhibited much better convergence with randomly initialized estimates.

For a visual reference, here are 3D scatter plots of samples from the random benchmark results that you can zoom in and see the difference:

The results can be reproduced with this repo: https://github.com/ProfFan/expmap-benchmark

Important New Features & Bugfixes

In addition to the change in default Pose3 retract, which will now be the full exponential map, GTSAM has seen a steady stream of commits since the last release, 4.0.2, which has been there for more than 6 months. A summary of the most important issues and features is below:

• Robust noise model is ready for general usage
  • It can be used to replace RANSAC for some applications
  • For a gentle introduction, see this awesome tutorial by Varun Agrawal
• CombinedImuFactor serialization is now fixed
• The ISAM2 KITTI example has a C++ port, thanks Thomas Jespersen for the help!
• Now you can choose arbitrary MATLAB install prefix for the toolbox build
• Now you can make python-install to install the Python toolbox
• Now you can use the Conjugate Gradient solver in Python
• Now you can install GTSAM with pip if you only use the Python interface
• Added FrobeniusFactor and FrobeniusWormholeFactor for robust SFM applications
• Switched to in-place update of the diagonal Hessian in LM
  • expect a 3%-5% speedup, YMMV
• The Cython wrapper now can be built on Windows :)
  • Kudos @tuwuhs for the help!
• Fixed a few memory-related bugs detected by the LLVM sanitizer
  • Greatly improved stability

Finale

With over a hundred merged pull requests, we welcome you again on board the new release of GTSAM, GTSAM 4.0.3. We would like to thank all our contributors for their precious commits and bug reports. Finally, thank you for using GTSAM and please don’t hesitate to open an issue on GitHub if you found a bug!