What are Factor Graphs?
GTSAM Posts
By Frank Dellaert, @fdellaert on Twitter
[Cross-posting from our new sister-site, OpenSAM.org]
Many computational problems in robotics have an optimization problem at their core. For example, in simultaneous localization and mapping (SLAM) and many other estimation problems we are after a maximum a posteriori estimate, i.e., we try to maximize posterior probability of the variables given a set of measurements. When attempting to act optimally, we try to maximize a performance index, or conversely minimize a penalty function. And even in classical planning, we are trying to find an assignment to a set of discrete variables that minimizes the plan length or optimizes for some other desirable property of the plan.
In most of these optimization problems, the objective to be maximized or minimized is composed of many different factors or terms that typically are local in nature, i.e., they only depend on a small subset of the entire set of variables. For example, in a tracking application, a particular video frame only provides information about the position of a target at a particular time. At the next time step, a different variable is associated with the target. Of course, this depends on the parametrization chosen: if a track is globally parametrized, for example as a polynomial, this locality is destroyed.
A particularly insightful way of modeling this locality structure is using the concept of factor graphs. Factor graphs are a class of graphical models in which there are variables and factors. The variables represent unknown quantities in the problem, and the factors represent functions on subsets of the variables. Edges in the factor graph are always between factors and variables, and indicate that a particular factor depends on a particular variable.
There are three main advantages to using factor graphs when designing algorithms for robotics applications:
- They can represent a wide variety of problems across robotics.
- By laying bare the compositional structure of the problem, they expose opportunities to improve computational performance.
- They are beneficial in designing and thinking about modelling your problem, even aside from performance considerations.
Because many optimization problems in robotics have the locality property, factor graphs can model a wide variety of problems across AI and robotics. Some of these are illustrated below:
Boolean Satisfiability:
In Boolean Satisfiability, we are looking for an assignment to Boolean variables that make a set of Boolean formulas true. In the example below, the rather boring looking Boolean equations is represented by the Boolean factor graph below:
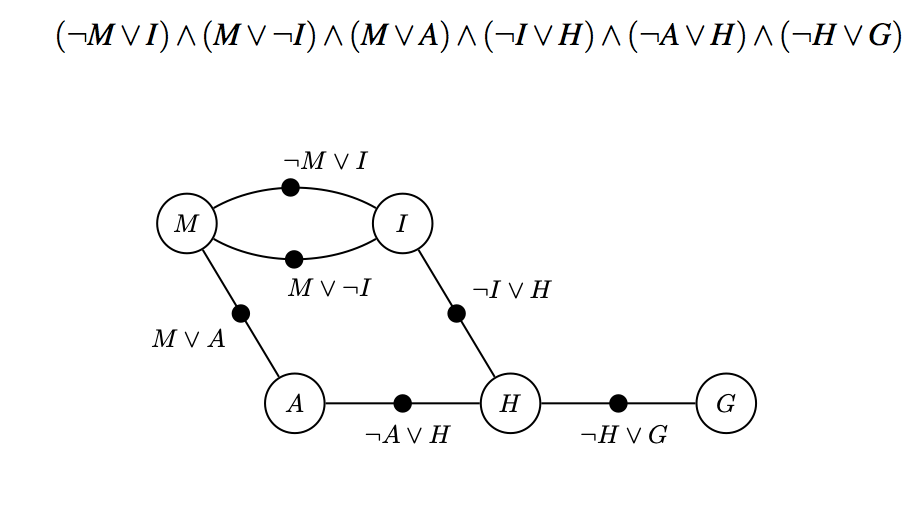
Constraint Satisfaction:
When we generalize from Boolean to discrete variables, we obtain the class of Constraint Satisfaction Problems or CSPs. For example, the image below shows a graph coloring problem where the goal is to assign a color (chosen from a finite set of colors) to the Swiss cantons such that no neighboring canton has the same color. In the graph below, these pairiwse constraints are indicated by the square factors.
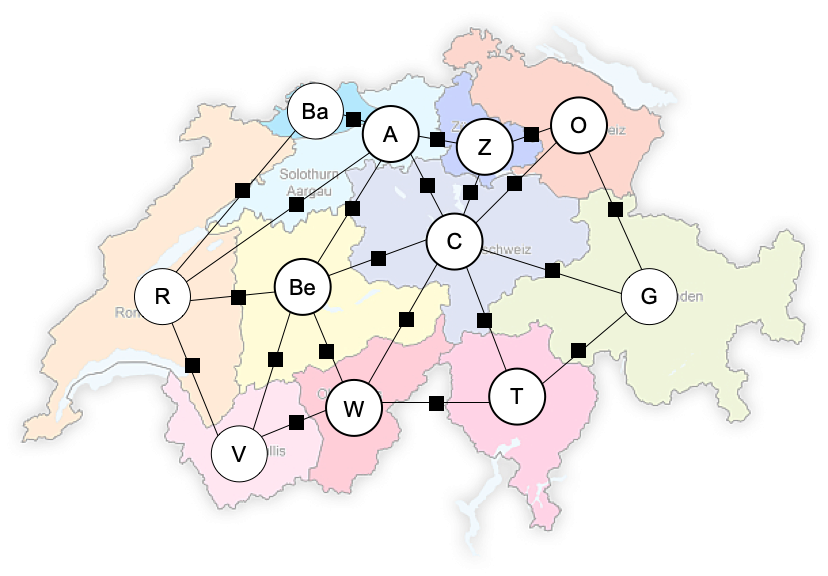
Bayes Networks:
If we relax the hard constraints to real-valued preferences, we switch to a Constraint Optimization Problem. This can be used to express that a particular color is preferred over another one. It can be shown that COPs are also the main optimization problem to solve in the venerable AI technique of Bayes networks. Below an example where a Bayes network with given evidence (the square nodes) is converted to a COP factor graph, which can then give the maximum probable explanation for the remaining (non-evidence) variables.
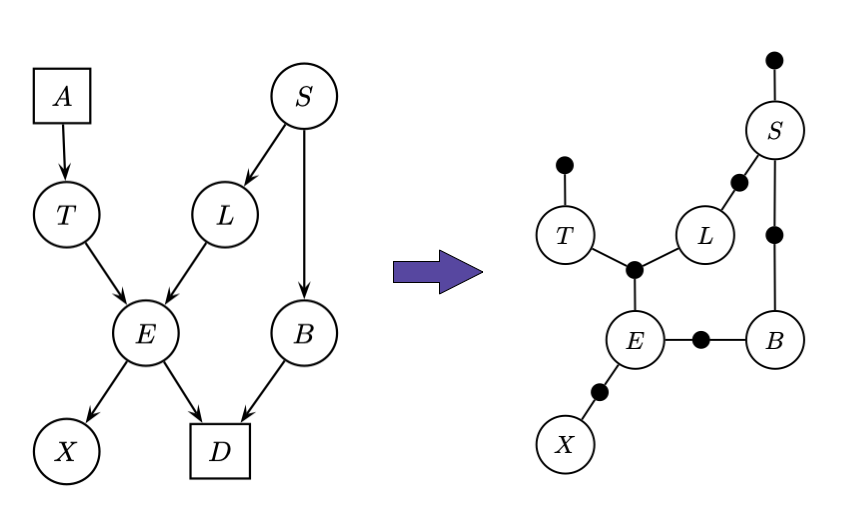
Polynomial Equations:
The constraints can also be other functions of the variables. For example, we can represent a system of polynomial equations by a factor graph. The example below, adapted from Gim Hee Lee’s Ph.D. thesis, encodes a minimal geometry problem from computer vision, useful for autonomous driving:
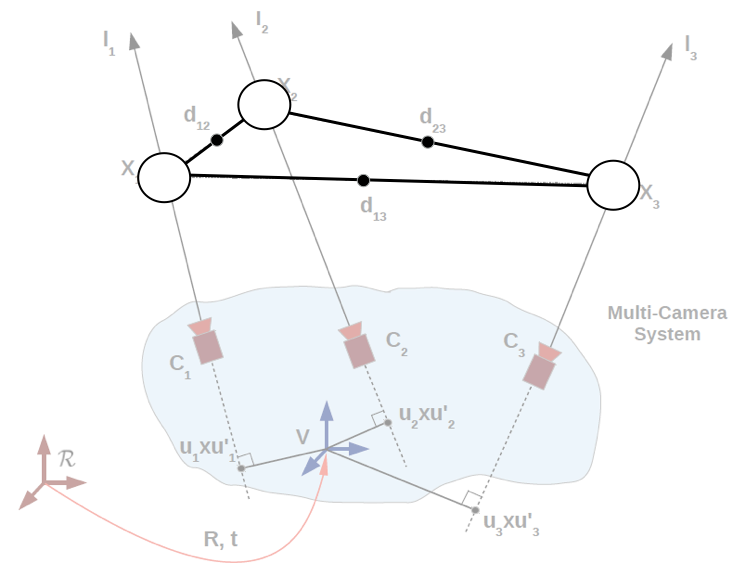
Simultaneous Localization and Mapping:
Speaking of autonomous driving, perhaps the most famous application of factor graphs is in SLAM, or Simultaneous Localization and Mapping. This is illustrated in the example below, where the location of a vehicle over time (the cyan variables) as well as the location of a set of landmarks (the dark blue nodes) are solved for. In this case we have a plethora of factors associated with vehicle odometry, landmark sightings, and GPS priors. The example in question is a small excerpt from a real robot experiment in Sydney’s Victoria Park.

Structure from Motion:
Finally, we can also represent 3D mapping or 3D reconstruction problems with factor graphs. Below we show just the edges in the factor graph connecting one camera (yellow) with all points visible from that camera (black) in a large-scale 3D reconstruction of downtown Chicago.

Conclusion
For more information about how factor graphs are typically used to solve perception problems in robotics, see the following booklet: Factor graphs for robot perception, by Frank Dellaert and Michael Kaess, which appeared in 2017 in Foundations and Trends in Robotics.
However, this is just the tip of the iceberg. Factor graphs can be used to model a much wider variety of problems across robotics domains, such as Tracking, Inertial Navigation, Mapping with LIDARs, Classical Planning, Reinforcement Learning and Optimal Control, Motion Planning etc…